常微分方程式の数値解法基礎

Math Physics

常微分方程式の数値解法のうち基礎的な手法をまとめました。

はじめに

3DCGで物理シミュレーションを行う際には常微分方程式を解く必要が出てきます。
しかしながら常微分方程式のうち解析的に解くことのできる問題は少ないため、 漸化式を用いて逐次計算を行う数値解法を用いることになります。

常微分方程式の数値解法はその性質上結果に誤差が生じ、その誤差を小さくするため多くの手法が存在します。
また手法により計算速度も異なるので、用途に応じて適したものを選択する必要があります。

そこで本記事ではこの常微分方程式の数値解法について、いくつかの基礎的な手法をまとめます。

オイラー法

最初に最もシンプルな方法であるオイラー法について説明します。
まず常微分方程式の解を y=y(x)としたとき、 x_{i}の周りでテイラー展開すると以下の式を得られます。

{\displaystyle y_{i+1}=y(x_{i}+\Delta x)=y(x_{i})+\frac{dy}{dx}\Delta x+\frac{1}{2} \frac{d^{2}y}{dx^{2}}\Delta x^{2}+\cdot \cdot \cdot \tag{1} }

ここで、

{\displaystyle \frac{dy}{dx} = f(x, y) \tag{2} }

とすると式(1)は以下のように表せます。

{\displaystyle y_{i+1}=y(x_{i})+f(x_{i}, y_{i}) \Delta x+O(\Delta x^{2}) \tag{3} }

ここで \Delta xが十分に小さいとすると、上式においてランダウの記号であらわしている項は無視できるので、

{\displaystyle y_{i+1}=y(x_{i})+f(x_{i}, y_{i}) \Delta x \tag{4} }

オイラー法はこのようにシンプルな式で計算できますが、その分誤差が多い方法となります。
試しに f(x)=sin(x)をこの方法で解くと、以下のような結果となります。

f:id:halya_11:20200330000007p:plain

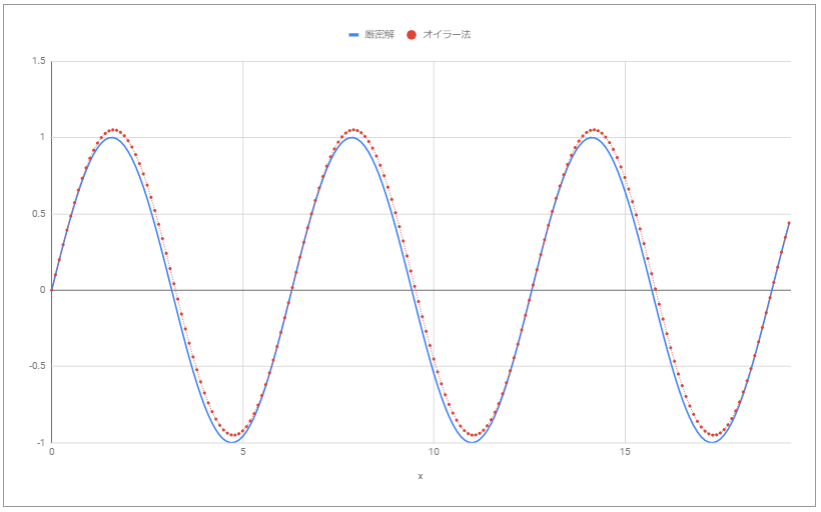
微妙に誤差があることが見て取れます。

ホイン法

前節のオイラー法は精度が悪いため、より精度の良い方法としてホイン法があります。
ホイン法は2次のルンゲクッタ法と呼ばれる手法のうちの一つという位置づけになります。

オイラー法の精度の悪さは i+1時点の解を求めるために i時点での値（傾き）を用いている点にあるので、
ホイン法では以下のように i+1時点の値も計算に組み込みます。

{\displaystyle y_{i+1}=y(x_{i})+\frac{1}{2}f(x_{i}, y_{i}) \Delta x+\frac{1}{2}f(x_{i+1}, y_{i+1}) \Delta x \tag{5} }

この i+1の値は前節のオイラー法により求めます。

f:id:halya_11:20200330003510p:plain
ホイン法

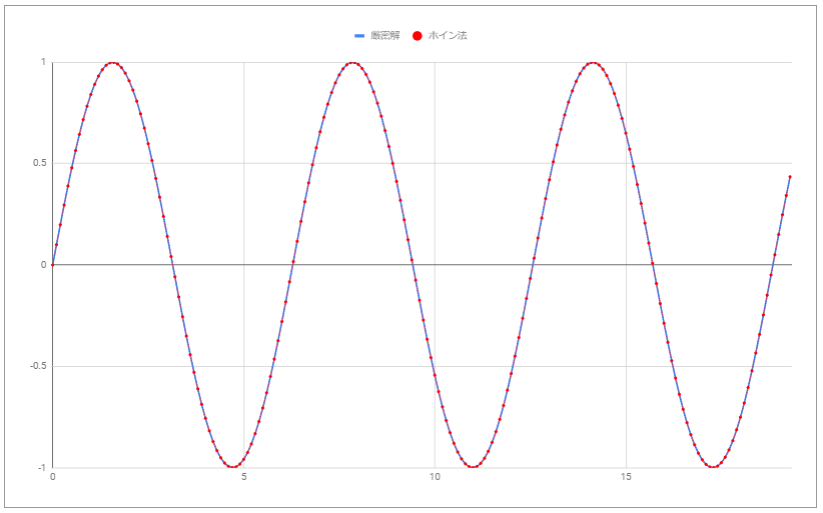
このケースでは前節の結果に比べてかなり誤差が目立たなくなりました。

4次のルンゲクッタ法

より精度の高い結果を得やすい方法として4次のルンゲクッタ法という手法があります。
これもさらにいくつかの手法に分かれるのですが、本記事ではこのうちの一つである4段4次の公式を紹介します。

4段4次のルンゲクッタ法ではまず以下のように k_{1}から k_{4}の値を求めます。

{\displaystyle k_{1}=f(x_{i},y_{i})\Delta x \tag{6} }

{\displaystyle k_{2}=f(x_{i}+\frac{\Delta x}{2},y_{i}+\frac{k_{1}}{2})\Delta x \tag{7} }

{\displaystyle k_{3}=f(x_{i}+\frac{\Delta x}{2},y_{i}+\frac{k_{2}}{2})\Delta x \tag{8} }

{\displaystyle k_{4}=f(x_{i}+ \Delta x ,y_{i} + k_{3})\Delta x \tag{9} }

次にこれらの値を使って以下の式により解を求めます。

{\displaystyle y_{i+1}=y_{i}+\frac{1}{6}(k_{1}+2k_{2}+2k_{3}+k_{4}) \tag{10} }

この手法を用いると前節までの方法に比べて \Delta xがある程度大きくても誤差の少ない結果を得られますが、
見ての通り計算コストも大きいため、目的に適した手法を選択する必要があります。

参考

www.yamamo10.jp