光の単位を勉強するうえで立体角の概念を理解する必要が出てきたので立体角についてまとめます。
まず平面角の定義
立体角を考える前にまず平面角について考えます。
平面角とは、普段「角度」と言っているあれです。分度器で測れるあれです。
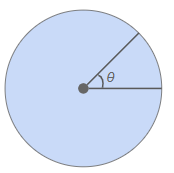
ここで、平面角180度を弧度法で表すとπ(ラジアン)になります。
そしてそうなると、当然ですが360度を弧度法で表すと2πになります。

次にふと半径1の円の円周を計算してみます。
円周は2πrで計算できるので、半径1の円の円周は2πになります。

ここで、360度を弧度法で表した「2π」と半径1の円周「2π」が同じであることに気づきます。
実はこれは偶然同じになったのではなく、そもそも平面角が「その角度が半径1の円から切り取る弧の長さ」として定義されているからなのです。
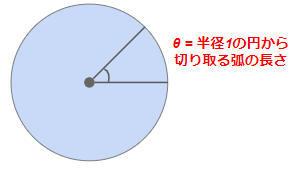
「そもそもなぜ360度が弧度法で2πなのか」ってあまり考える機会がありませんが、実はこういう定義なのです。
立体角は平面角を3次元に拡張したもの
さていよいよ本題の立体角です。
立体角は平面角の考え方を三次元に拡張したものです。
「円」を三次元に拡張すると「球」になり、「弧」を三次元に拡張すると「表面積」になります。
よって立体角の定義は「その角度が半径1の球から切り取る表面積の大きさ」となります。

直観的な定義としては下記の表記がわかりやすいです。
ある点からの広がりの大きさを表す 立体角の意味と計算の例 - 具体例で学ぶ数学
また、球の表面積は4πなので、すべての方向を表すような立体角は4πとなります。
単位は、平面角のラジアンに対してステラジアン(sr)を使います。