【Unity】法線は陰関数を偏微分すれば求められるという話

法線は陰関数を偏微分すれば求められるという話です。

法線は陰関数を偏微分すれば求められる
プログラムで書いてみる
三次元に応用する
三次元もプログラムで書いてみる
参考

Unity2019.1.0

法線は陰関数を偏微分すれば求められる

いま、次の通り円の方程式を考えます。

${ \displaystyle x^{2} + y^{2} = r^{2} }$

このようなyがxの関数じゃない形式の関数を陰関数と呼びます。
この陰関数を偏微分すると法線が求められます。
まず、xについて偏微分します。

${ \displaystyle f_{x}=2x }$

同様にyについても偏微分します。

${ \displaystyle f_{y}=2y }$

面白いことに、これらがそのまま法線を表します。
すなわち法線は以下の通りとなります。

${ \displaystyle (2x, 2y) }$

この導出は本筋から外れるので本記事では行いませんが、下記のサイトで分かりやすく解説されています。

mathtrain.jp

プログラムで書いてみる

それではこの公式をプログラムで確認してみます。

using UnityEngine;

public class Example : MonoBehaviour
{
    private Vector2[] _positions;
    private Color[] _colors;

    private void Start()
    {
        // 円上の位置をランダムに取得する
        // 色も適当に作っておく
        var capacity = 100;
        _positions = new Vector2[capacity];
        _colors = new Color[capacity];
        for (int i = 0; i < _positions.Length; i++) {
            _positions[i] = GetRandomPositionOnCircle();
            _colors[i] = Random.ColorHSV();
        }
    }

    private void OnDrawGizmos()
    {
        if (!Application.isPlaying) {
            return;
        }
        var gizmoColor = Gizmos.color;
        for (int i = 0; i < _positions.Length; i++) {
            Gizmos.color = _colors[i];
            var position = _positions[i];
            // 位置に球を描画
            var drawPos = new Vector3(position.x, 0, position.y);
            Gizmos.DrawSphere(drawPos, 0.04f);
            // 法線を偏微分の結果から取得して線を描画
            var normal = GetNormal(position);
            var drawNormal = new Vector3(normal.x, 0, normal.y);
            Gizmos.DrawLine(drawPos, drawPos + drawNormal * 0.3f);
        }
        Gizmos.color = gizmoColor;
    }

    /// <summary>
    /// 円上の位置をランダムに取得する
    /// </summary>
    private Vector2 GetRandomPositionOnCircle()
    {
        Vector2 result = Random.rotation * Vector3.one;
        result.Normalize();
        return result;
    }

    /// <summary>
    /// 当該位置における法線を取得する
    /// </summary>
    private Vector2 GetNormal(Vector2 position)
    {
        position.x *= 2;
        position.y *= 2;
        return position;
    }
}

円上の点を適当に取ってきて球体を描画しています。
また円の方程式を陰関数にして偏微分したものから法線を計算し、線を描画しています。

結果は次のようになりました。

f:id:halya_11:20190719005134p:plain

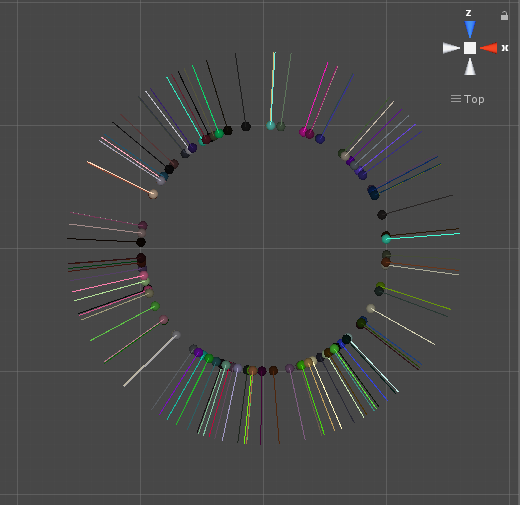
ちゃんと法線が計算できていることが確認できました。

三次元に応用する

この公式は三次元でも同様です。
例えばいま楕円体の方程式を考えます。
Wikipediaによると楕円体の方程式は下記のような感じらしいです。

${ \displaystyle \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} + \frac{z^{2}}{c^{2}} = 1 }$

これを二次元のときと同様に偏微分します。

${ \displaystyle f_{x}=\frac{2x}{a^{2}} }$

${ \displaystyle f_{y}=\frac{2y}{b^{2}} }$

${ \displaystyle f_{z}=\frac{2z}{c^{2}} }$

これで法線が求められました。

三次元もプログラムで書いてみる

それではこちらもプログラムで書いてみます。

using UnityEngine;

public class Example : MonoBehaviour
{
    private const float ELLIPSOID_A = 1.0f;
    private const float ELLIPSOID_B = 1.0f;
    private const float ELLIPSOID_C = 2.0f;
    private Vector3[] _positions;
    private Color[] _colors;

    private void Start()
    {
        // 楕円体上の位置をランダムに取得する
        // 色も適当に作っておく
        var capacity = 500;
        _positions = new Vector3[capacity];
        _colors = new Color[capacity];
        for (int i = 0; i < _positions.Length; i++) {
            _positions[i] = GetRandomPositionOnEllipsoid();
            _colors[i] = Random.ColorHSV();
        }
    }

    private void OnDrawGizmos()
    {
        if (!Application.isPlaying) {
            return;
        }
        var gizmoColor = Gizmos.color;
        for (int i = 0; i < _positions.Length; i++) {
            Gizmos.color = _colors[i];
            var position = _positions[i];
            // 位置に球を描画
            Gizmos.DrawSphere(position, 0.08f);
            // 法線を偏微分の結果から取得して線を描画
            var normal = GetNormal(position);
            Gizmos.DrawLine(position, position + normal * 0.3f);
        }
        Gizmos.color = gizmoColor;
    }

    /// <summary>
    /// 楕円体上の位置をランダムに取得する
    /// </summary>
    private Vector3 GetRandomPositionOnEllipsoid()
    {
        var theta = Random.Range(0.0f, Mathf.PI);
        var phi = Random.Range(0.0f, Mathf.PI * 2);
        var result = Vector3.zero;
        result.x = ELLIPSOID_A * Mathf.Sin(theta) * Mathf.Cos(phi);
        result.y = ELLIPSOID_B * Mathf.Sin(theta) * Mathf.Sin(phi);
        result.z = ELLIPSOID_C * Mathf.Cos(theta);
        return result;
    }

    /// <summary>
    /// 当該位置における法線を取得する
    /// </summary>
    private Vector3 GetNormal(Vector3 position)
    {
        position.x = 2 * position.x / Mathf.Pow(ELLIPSOID_A, 2.0f);
        position.y = 2 * position.y / Mathf.Pow(ELLIPSOID_B, 2.0f);
        position.z = 2 * position.z / Mathf.Pow(ELLIPSOID_C, 2.0f);
        return position;
    }
}