ガウス関数を使うにはその性質だけわかっていれば十分なことが多いです。
この記事では難しい話は置いておいて、知っておくべきガウス関数の性質だけをまとめました。
はじめに
グラフィックスの処理を読んでいるときに時々ガウス関数を見かけます。
しかしガウス関数は、調べようとするといきなりわけのわからない理論と式が出てきて嫌になってしまいます。
ガウス関数は複雑な式ではありますが、プログラムで使う分にはそんなに高尚な知識は必要ありません。
要はどの変数をいじったらどのようにグラフが変化するかを理解していればよさそうです。
そこで難しい説明は他サイトに任せて、ここではガウス関数の性質だけ追ってみます。
ガウス関数?
さてガウス関数とはこんな感じの釣鐘型を示す関数です。

式は例えばこのようになります。
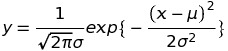
いきなりわけのわからない式ですが、この時点ではとりあえずyがxの関数だってことだけわかれば大丈夫です。
ちなみに今回はWikipediaに載っている正規分布関数を使っています。
1. μを変えてみる
さてそれではここから各変数をいじってグラフがどのように変化するかを見ていきます。
まずμを変えてみます。

ここをいろんな値に変えると、

横にずれます。
μの値は釣鐘型の中央位置を表しています。
μ=0なら中央の位置もゼロ。
2. σを変えてみる
次にσを変えてみます。

前節のμをゼロに固定して、この値をいろいろと変えると、

なだらかさが変わります。
σが大きいほどなだらか。
3. 定数をなくす

赤枠の定数部分をなくす、というか1に置き換えてみます。

最大値がすべて1になりました。
ちなみに今回1に置き換えたこの定数部分には、関数の積分値を一定(1)にするという役割があります。
まとめ
ガウス関数の性質をまとめてみました。
とりあえずこれだけ知っておけば十分ではないかと思います。
シェーダでの使い方は別の記事で紹介します。